慣性モーメントとは?
2021年2月27月更新
慣性モーメントってなんだろう
大学の物理で初めて登場する慣性モーメント.教科書にはよく
\[
I = \int r^2dm
\]
と書かれているけれど,これっていったいどんな意味があるんだろう.
端的に言えば物体の回転しにくさを表す量ってだけなんですが,こういうのって授業中にポンといきなり式だけ与えられるように感じますよね.
で,モーメントが~角運動量が~と話が進んでいって,物理的なイメージが湧かずに置いてけぼりになって戸惑う人も多いと思います.
一方で,慣性モーメントは実際に機械を設計する上でも重要です.特に振動やロボットをやる場合にはよく出てきます.
エネルギー研究部で開発している電気自動車でも,機械部品の慣性モーメントを考えることが重要な問題だったりします.
そこで,本記事では慣性モーメントについて直観的なイメージを持ってもらうことを目標に,質点の回転を題材として慣性モーメントの基本的な考え方を解説していきます.
前提として,高校で習う物理の基本的なこと($ma = F$や力のモーメントなど)が分かっていれば読み進められると思います.
読み物として気軽に読めるような感じを目指して書きました.
直観的なわかりやすさを重視したので数学的な厳密さが犠牲になっている箇所もありますが,全体的な流れを追っていけば特段問題はないと思います.
目次
1. どっちが回すの大変?
2. 準備:ニュートンの運動の法則
3. ある軸まわりを質点が回転するときの慣性モーメント
1. どっちが回すの大変?
図1のような2種類の輪っかを回すことを考えてみましょう.
一方は直径3.0 $\mathrm{m}$,もう一方は直径0.50 $\mathrm{m}$として,質量はどちらも20 $\mathrm{kg}$とします.
回転軸は水車のように固定されているものとします.
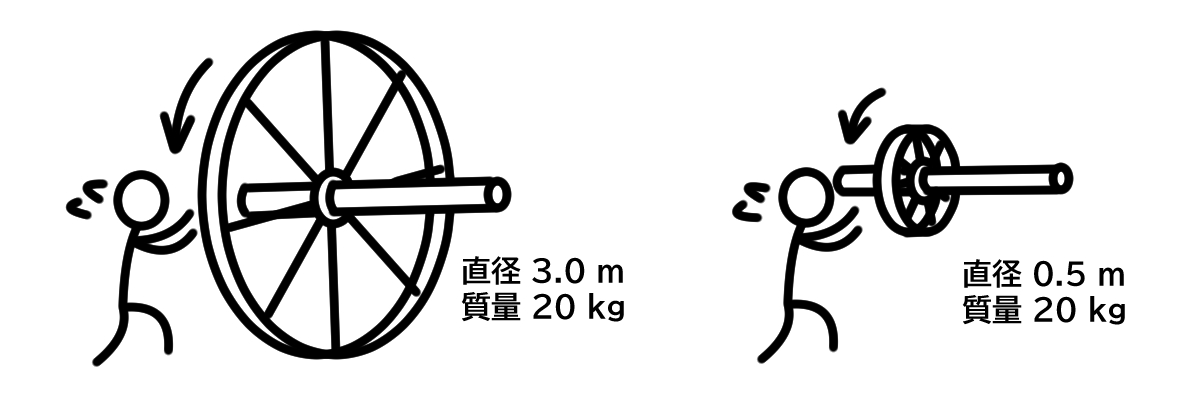
図1. どちらが回しにくそう?
さて,この2種類の輪っかのうち,どちらが回すときに力が必要でしょうか.
どちらが止めるときに力が必要でしょうか.
実際に手で回す,あるいは止めることを想像してみてください.
結論だけ言うと,直径3.0 $\mathrm{m}$の輪っかのほうが回しにくく,止めにくいです.
読者のみなさんも,ぱっと直観的に答えがわかったことと思います.
慣性モーメントはこのような物体の回しにくさ,止めにくさを決める量で,その値が大きいほど回しにくく,止めにくいです.
では,なぜ慣性モーメントなる値が大きいと回しにくく止めにくいのでしょうか.
この "回しにくさ","止めにくさ" を決定する物理的な根拠とは一体なんなのでしょうか.
以下の章でそれを考えていきます.
2. 準備:ニュートンの運動の法則
話に入る前の準備として,ニュートンの運動の法則についてすこし触れます.
ニュートンの運動の法則は次の3つの法則から構成されています.
第1法則;外から力を受けない物体は,静止しているか等速直線運動を続ける(慣性の法則)
第2法則;物体に力を加えると,物体にはその質量に反比例した加速度が生じる(ニュートンの運動方程式)
第3法則;物体Aが物体Bに力を加えているとき,物体Aは物体Bから同じだけの力を受ける(作用・反作用の法則)
特に,第2法則について述べたいと思います.
質量を$m$,加速度を$a$,力を$F$とすると
\[
ma = F \; \; \; \dotsb \dotsb (1)
\]
という関係が成り立ちますが,これをニュートンの第2法則と呼びます.
式(1)は「質量$m$の物体に力$F$を加えたとき,物体は加速度$a$で動く」ということを意味しています.
質量が大きいほど,同じ加速度で物体を動かすには大きな力が必要だということがわかります.
式(1)は物体の動かしにくさを表しているんですね.
ここで,速度を$v$とすれば,加速度$a$は
\[
a = \frac {dv}{dt} \; \; \; \dotsb \dotsb (2)
\]
と書けるので,式(1)と式(2)より
\[
m\frac {dv}{dt} = F \; \; \; \dotsb \dotsb (3)
\]
と書けます.
式(3)を変形して,次の関係が導かれます.
\[
\frac {d}{dt}(mv) = F \; \; \; \dotsb \dotsb (4)
\]
式(4)は高校の物理で習う力積の公式,$F\Delta t = mv_2 - mv_1$と同じことを意味する式です.
このことから,物体の運動量が変化するとき,物体には何かしらの力が作用しているということがわかります.
言い換えれば,物体の運動量を変化させるには,物体に力を加えないといけないということですね.
3. ある軸まわりを質点が回転するときの慣性モーメント
さて,本題に入ります.
大きさ(つまり体積)が無視できる質量$m$の質点が,ある軸(ここではz軸)まわりを回転している状況を考えてみましょう(図2).
簡単のために,ここでは質点がz軸まわりを一定の半径$r$で回転するものとします.
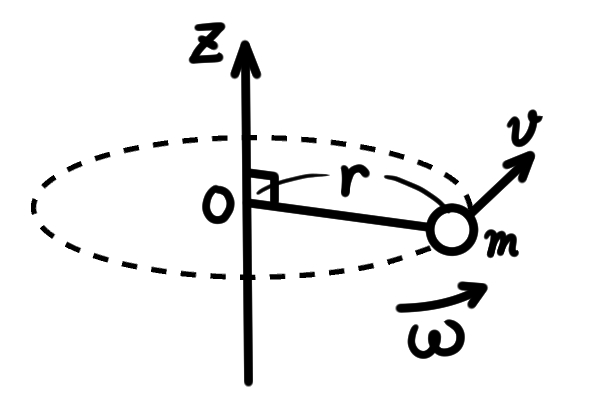
図2. z軸まわりを円運動する質点
図2を上から見たものを図3に書き直します.
質点が時刻$t$に速度$v(t)$,角速度$\omega(t)$で$z$軸まわりを回転しています.
$\Delta t$後に速度$v(t + \Delta t)$,角速度$\omega(t + \Delta t)$で$z$軸まわりを回転したとします.
このとき,質点の運動量の変化は次のようになります.
\[
mv(t + \Delta t) - mv(t) \; \; \; \dotsb \dotsb (5)
\]
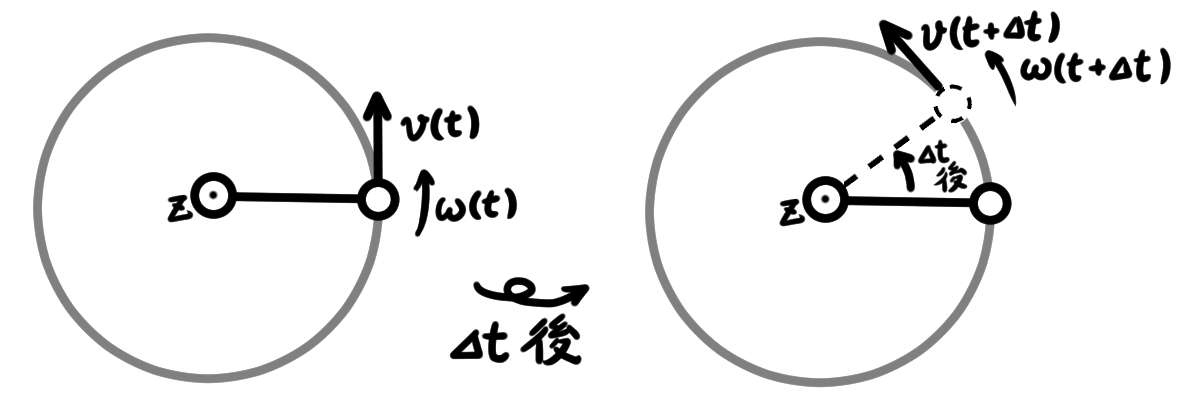
図3. 質点の運動の時間変化
回転半径は$r$で一定なので,質点の円弧を描いて回転します.
質点が外から力を受けない場合,慣性の法則から,質点は等速円運動します.
このとき質点が受けるのは,一定の力で作用する向心力(遠心力)のみです.
質点の回転速度を変化させるには,質点に外から何かしらの力を運動の接線方向に加えてやる必要があります.
例えば質点を加速させる向き(質点の進行方向,円弧の接線方向)に外力が作用すると,質点の回転速度は増加します.
このとき作用・反作用の法則から,質点は回転速度の変化を妨げようとする力,つまり反力として,自身に加られらえたのと同じだけの力を質点の進行方向と逆方向に受けます.
反対に質点を減速させる向き(質点の進行方向と逆方向,円弧の接線方向)に外力が作用すると,質点の回転速度は減少します.
このとき作用・反作用の法則から,質点は回転速度の変化を妨げようとする力,つまり反力として,自身に加られらえたのと同じだけの力を質点の進行方向と同じ方向に受けます.
さて,$\Delta t$間に質点に力$F$を加えたとき,質点の運動量が$mv(t)$から$mv(t + \Delta t)$に変化したとすると(図3)
\[
\frac{mv(t + \Delta t) - mv(t)}{\Delta t} = F \; \; \; \dotsb \dotsb (6)
\]
と書けます.
ここで,力$F$は
「$\Delta t$間に質点の運動量を$mv(t)$から$mv(t + \Delta t)$に変化させるのに必要な力」
ですが,作用・反作用の法則から,その大きさは
「$\Delta t$間に質点の運動量を$mv(t)$から$mv(t + \Delta t)$に変化させるときに,質点の運動の変化を妨げる力」
と等しくなります.
$\Delta t$をとても小さいものとして考えて,$\Delta t \to 0$で極限をとれば
\[
\lim_{\Delta t \to 0}\frac{mv(t + \Delta t) - mv(t)}{\Delta t} = F \; \; \; \dotsb \dotsb (7)
\]
となります.
微分の定義(高校数学でいう数Ⅲの範囲で習うと思います)から
\[
\lim_{\Delta t \to 0}\frac{mv(t + \Delta t) - mv(t)}{\Delta t} = \frac {d}{dt}(mv) \; \; \; \dotsb \dotsb (8)
\]
と書けるので,式(7)と式(8)から
\[
\frac {d}{dt}(mv) = F \; \; \; \dotsb \dotsb (9)
\]
となり,式(4)と同じ式を得ます.
ここで,周速は回転半径と角速度の積なので
\[
v = r\omega \; \; \; \dotsb \dotsb (10)
\]
よって,式(10)を式(9)に代入して次式を得ます.
\[
\frac {d}{dt}(mr\omega) = F \; \; \; \dotsb \dotsb (11)
\]
式(11)を変形して
\[
mr\frac {d\omega}{dt} = F \; \; \; \dotsb \dotsb (12)
\]
時間の1階微分を,文字の上に1つドットを付けて表すことにすると
\[
\frac {d\omega}{dt} = \dot \omega \; \; \; \dotsb \dotsb (13)
\]
となるので,式(13)を式(12)に適用して
\[
mr\dot \omega = F \; \; \; \dotsb \dotsb (14)
\]
と書けます.
もう一度述べますが,この力$F$は質点の回転速度$v$(角速度$\omega$)を変化させるのに必要な力です.
式(14)は,半径$r$で円運動する質量$m$の質点を角加速度$\dot \omega$で回転させるには,質点の軌道の接線方向に力$F$を加えてあげてくださいね,と言っています.
質点の回転速度$v$(角速度$\omega$)を変化させるのに必要なトルクを$T$とすると
\[
Fr = T \; \; \; \dotsb \dotsb (15)
\]
と書けます.力かける距離,高校物理でいうところの力のモーメントですね.
回転軸まわりの力のモーメントのことを特に "トルク" と言います.
式(14)と式(15)より,物体の回転速度$v$(角速度$\omega$)を変化させるのに回転軸に加えるべきトルク$T$は
\[
mr^2\dot \omega = T \; \; \; \dotsb \dotsb (16)
\]
と表せます.
ここでInertia(慣性)の頭文字をとって
\[
I = mr^2 \; \; \; \dotsb \dotsb (17)
\]
とすると,式(16)と式(17)から
\[
I\dot \omega = T \; \; \; \dotsb \dotsb (18)
\]
と書けます.この$I$を慣性モーメントと呼びます.
さて,式(1)を見ると
\[
ma = F
\]
とあります.
この式と式(18)を見比べると,なんだか似ているように感じませんか?
式(1)は
「物体に力$F$を加えると,物体はその質量$m$に反比例した加速度$a$で運動する」
ということを意味していました.
対して式(18)は
「物体の回転軸まわりにトルク$T$を加えると,物体はその慣性モーメント$I$に反比例した角加速度$\dot \omega$で回転する」
ということを意味します.
つまり,慣性モーメント$I$は質量$m$と同じような役割をしているんですね.対応関係を表1に示します.
| 表1. 対応関係 |
| 並進運動 |
回転運動 |
| 力$F$ [$\mathrm{N}$] |
トルク$T$ [$\mathrm{Nm}$] |
| 質量$m$ [$\mathrm{㎏}$] |
慣性モーメント$I$ [$\mathrm{kgm^2}$] |
| 加速度$a$ [$\mathrm{m/s^2}$] |
角加速度$\dot \omega$ [$\mathrm{rad/s^2}$] |
いかがでしたでしょうか.
慣性モーメントは一見すると全く新しく出てきた概念のように感じてしまいますが,本質は私たちがこれまで慣れ親しんできた$ma = F$と一緒だということがわかったと思います.
この記事によって読者の慣性モーメントへの理解が深まってくれたら幸いです.
記事一覧へ戻る
トップへ戻る


